| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 항해99
- 코딩테스트준비
- 예외클래스
- 개발자취업
- 예외
- 일반 예외
- 실행 예외
- 예외 처리
- 99클럽
- try-catch-finally 블록
- throws 키워드
- 다중 catch 블록
- til
- 로켓펀치 #취준컴퍼니 #취업 #일상 #취준생
- Today
- Total
innn
시간 복잡도 활용하기 본문
그렇다면 시간 복잡도의 개념을 코딩 테스트에선 어떻게 활용해야 할까?
알고리즘 선택의 기준으로 사용하기
정렬 부분의 학습을 완료했고 버블 정렬, 병합 정렬의 시간 복잡도를 각각 O(n^2), O(nlogn)이라고 알고 있다고 가정하자.
연습문제 000_수 정렬하기
n개의 수가 주어졌을 때 이를 오름차순으로 정렬하는 프로그램을 작성하시오. (시간 제한 2초)
- 입력
1번째 줄에 수의 개수 N(1 <= N <= 1,000,000), 2번째 줄부터는 N개의 줄에 숫자가 주어진다. 이 수는 절대값이 1,000,000보다 작거나 같은 정수다. 수는 중복되지 않는다.
- 출력
1번째 줄부터 N개의 줄에 오름차순 정렬한 결과를 1줄에 1개씩 출력한다.
예제 입력 1
5
5
2
3
4
1
예제 출력 1
1
2
3
4
5
시간 제한이 2초이므로 이 조건을 만족하려면 2억 번 이하의 연산 횟수로 문제를 해결해야 한다. (기준 1억번에 1초)
따라서 문제에서 주어진 시간 제한과 데이터 크기를 바탕으로 어떤 정렬 알고리즘을 사용해야 할 것인지를 판단할 수 있따.
> 단, 연간 횟수는 1초에 1억 번 연산하는 것을 기준으로 생각한다.
> 시간 복잡도는 항상 최악일 때, 즉 데이터의 크기가 가장 클 때를 기준으로 한다.
연산 횟수 계산 방법
연산 횟수 = 알고리즘 시간 복잡도 X 데이터의 크기
위 공식을 대입해 각 알고리즘이 이 문제에 적합한지 판단해 보자
알고리즘 적합성 평가
- 버블 정렬 = (1,000,000)^2 = 1,000,000,000,000 > 200,000,000 → 부적합 알고리즘 (2억번 보다 크니까)
- 병합 정렬 = 1,000,000log(1,000,000) = 약 20,000,000 < 200,000,000 → 적합 알고리즘
근데 왜 병합정렬 1,000,000log(1,000,000) 이게 왜 20,000,000 이누? 6,000,000 아님?????
책이 이상한것 같음.. (이1지스 퍼1블리싱.. 오탈자 아닌가요 아니라면 죄송)
문제에 주어진 시간 제한이 2초이므로 연산 횟수 2억 번 안에 원하는 답을 구해야한다.
버블 정렬은 약 10억 번의 연산횟수가 필요하므로 부적합하다.
병합 정렬은 약 2,000만 번(600만 번 아닌지...)의 연산 횟수로 답을 구할 수 있어 적합한 알고리즘이다.
이와 같이 시간 복잡도 분석으로 문제에서 사용할 수 있는 알고리즘을 선택할 수 있고,
이 범위를 바탕으로 문제의 실마리를 찾을 수 있다.
즉, 데이터의 크기(N)를 단서로 사용해야하는 알고리즘 추측해 볼 수 있는 것이다.
시간 복잡도를 바탕으로 코드 로직 개선하기
시간 복잡도는 작성한 코드의 비효율적인 로직logic을 개선하는 바탕으로도 사용할 수 있다.
이 부분을 활용하려면 가장 먼저 코드의 시간 복잡도를 도출할 수 있어야 한다. 시간 복잡도를 도출하려면 다음 2가지 기준을 고려해야한다.
시간 복잡도 도출 기준
- 상수는 시간 복잡도 계산에서 제외한다.
- 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
코드로 예를 들어 보자.

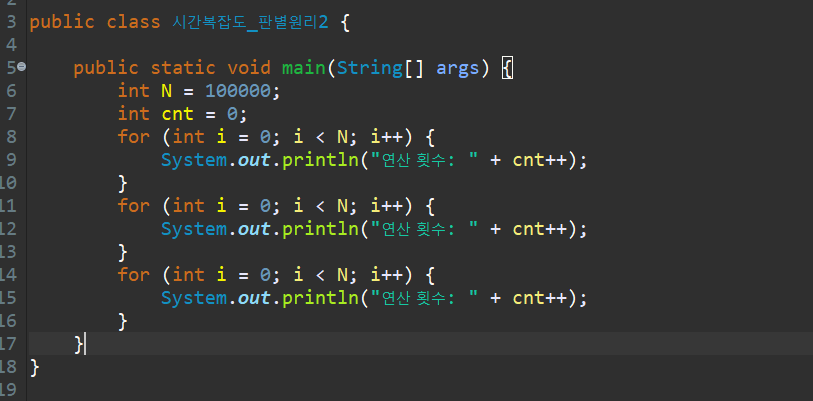
두 예제 코드의 연산 횟수는 3배의 차이가 난다. 언뜻 생각하면 큰 차이인 것 같지만 코딩 테스트에서는 일반적으로 상수를 무시하므로 두 코드의 시간 복잡도는 O(n)으로 같다.
다음 예제 코드를 확인해보자.
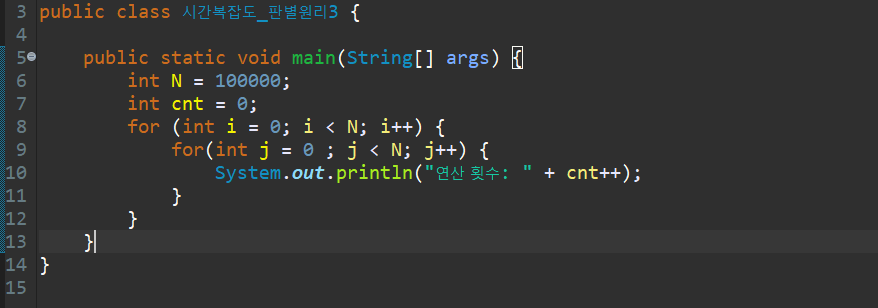
시간 복잡도는 가장 많이 중첩된 반복문을 기준으로 도출하므로 이 코드에서 이중 for 문이 전체 코드의 시간 복잡도 기준이 된다. 만약 일반 for 문 10개가 더 있다 하더라도 도출 원리의 기준 2번(가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다)에 따라 시간 복잡도의 변화 없이 N^2으로 유지된다.
이와 같이 자신이 작성한 코드의 시간 복잡도를 도출할 수 있다면, 실제 코테에서도 시간 초과가 발생했을 때 이 원리를 바탕으로 문제가 되는 코드 부분을 도출할 수 있고, 이 부분을 연산에 더욱 효율적인 구조로 수정하는 작업으로 문제를 해결할 수 있다.
'코딩 테스트 > 코테 문제 풀이' 카테고리의 다른 글
| 배열과 리스트 (문제 002) (ArithmeticException 에러 뜻) (0) | 2022.09.25 |
|---|---|
| 배열과 리스트 (문제 001) (0) | 2022.09.24 |
| 디버깅 활용 사례 살펴보기 (0) | 2022.09.24 |
| 디버깅은 왜 중요할까 (0) | 2022.09.21 |
| 시간 복잡도의 개념 (0) | 2022.09.21 |




